La programmation est utilisée pour résoudre des problèmes. Ces derniers amènent souvent à analyser, lire, mémoriser des données. Nombre de ces petites opérations, qui effectuent des actions simples, basiques à l’échelle d’un algorithme, sont fréquemment utilisées. Pour réduire le temps de calcul (c’est-à-dire, le temps pour rendre un résultat) et l’espace en mémoire (le nombre d’informations à stocker pour faire les calculs), il est préférable de les organiser, selon le but à atteindre, dans un objet de type structure de données. Dans la majorité des langages, ces objets sont déjà implémentés (c’est-à-dire programmés) et prêts à l’usage. Une structure de données permet de définir clairement ces objets et de faciliter leur utilisation.

Définitions

En programmation, une structure de données est un type d’objet programmé qui répond à deux exigences :

• stocker des données de manière à faciliter et à optimiser en temps et en coût de stockage une opération en particulier (lecture, récupération d’un élément qui remplit un certain critère, …);

• posséder des primitives (des opérations “de base” sur cette structure de données) qui permettent notamment d’initialiser, de détruire, et de modifier cette structure de données.

Par exemple, un graphe n’est pas une structure de données en lui-même : c’est un objet mathématique, qui cependant peut nécessiter l’utilisation de structures de données, pour stocker ses arêtes et ses noeuds, dans le programme dans lequel le graphe est appelé.

Une structure de données en elle-même est un objet abstrait : les attributs qu’elle possède ne sont pas définis par leur implémentation, c’est-à-dire le code qui décrit la structure de données. Une structure de données peut avoir plusieurs implémentations, puisqu’il peut exister plusieurs façons d’effectuer une même action. Par exemple, si l’on souhaite stocker les interactions entre les noeuds d’un graphe (voir l’article sur les graphes pour plus de détails), on peut les écrire sous au moins deux formes :

• comme un tableau à double entrée : en nommant les colonnes et les lignes avec les identifiants de chaque noeud, on place un 1 dans chaque case où les noeuds correspondant à la colonne et à la ligne de la case sont reliés par une arête (dans le cas d’un graphe non orienté), sinon on y place un 0;

• comme un tableau à une seule dimension, de longueur égale au nombre de noeuds : pour chaque case nommée après le noeud N, on reporte chaque noeud qui est relié à N par une arête (dans le cas d’un graphe non orienté).

Par exemple, pour le graphe suivant :

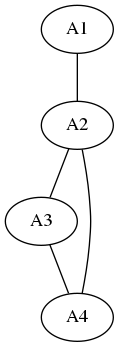
La première méthode donne le tableau suivant :

Indices	A1	A2	A3	A4
A1	0	1	0	0
A2	1	0	1	1
A3	0	1	0	1
A4	0	1	1	0

Cette structure de données s’appelle une matrice d’adjacence.

La deuxième méthode donne le tableau suivant :

A1	A2	A3	A4
A2;	A3, A4;	A2, A4;	A2, A3;

Cette structure de données s’appelle un tableau de listes d’adjacence.

Dans la suite de cet article, nous allons rencontrer deux autres types de structures de données, beaucoup plus fondamentaux : les listes et les tableaux. On verra la syntaxe utilisée dans le langage OCaml pour ces structures.

Les listes

Les listes ici sont plus exactement des listes simplement chaînées ici. Elles contiennent des éléments souvent de même nature, selon le langage de programmation utilisé : par exemple, que des entiers, que des nombres réels, etc. Ces éléments sont ordonnés : la liste commence par un élément de tête, et finit par un ensemble d’éléments appelés queue. La liste est construite de façon récursive : l’élément de tête est relié au premier élément de la queue (qui est lui-même, s’il existe, l’élément de tête de la queue) par un pointeur, c’est-à-dire un lien entre deux espaces mémoires de l’ordinateur. Depuis l’élément de tête, on peut accéder à l’élément de tête de la queue de la liste initiale, et depuis ce dernier, on peut à nouveau accéder à l’élément de tête du reste de la liste, etc. Le dernier élément de la liste est relié à un élément “vide”, appelé souvent nil, qui marque la fin de la liste.

Image de l’utilisateur Lasinki, Wikipédia

Le but des listes est de faciliter l’ajout et la suppression d’éléments (de tête) à stocker, au détriment de l’accès à un élément précis de la liste différent de l’élément de tête, par exemple.

Les primitives des listes comprennent les fonctions suivantes :

• concat (parfois aussi appelée push) : cette fonction ajoute un élément à la liste, en le plaçant comme élément de tête et en créant un pointeur de ce dernier vers l’ancien élément de tête. En OCaml, cette opération s’écrit de la façon suivante :

let liste = [1;2;3];;
let liste2 = 3 :: liste;;
liste2;;

retourne la liste [3;1;2;3].

• peek : cette fonction retourne l’élément de tête de la liste.

let liste = [1;2;3];;
let peek liste = match liste with
| [] -> failwith "La liste est vide !"
| t::q -> t;;
peek liste;;

retourne l’entier 1.

• pop : cette fonction retire l’élément de tête de la liste.

let liste = [1;2;3];;
let pop liste = match liste with
| [] -> failwith "La liste est vide !"
| t::q -> q;;
pop liste;;

retourne la liste [2;3].

Il existe d’autres structures de données qui perfectionnent les listes, par exemple les listes doublement chaînées, qui seront abordées dans un prochain article.

Les tableaux

Les tableaux sont à privilégier lorsque l’on veut accéder un élément précis du tableau rapidement (au détriment de l’ajout et de la suppression d’élément, qui nécessitent de recréer un nouveau tableau). Lorsqu’un tableau est créé, un espace mémoire fixé lui est dédié, et chaque élément du tableau est placé dans un espace mémoire/cellule donné(e). On accède à chaque élément en sélectionnant son adresse mémoire, et non en suivant un pointeur, comme fait dans les listes.

Les primitives pour les tableaux comprennent les fonction suivantes :

• set :

let tableau = [|1;2;3|];;
tableau.(1) <- 4;;
tableau;;

retourne le tableau [

1;4;3

].

• get :

let tableau = [|1;2;3|];;
tableau.(1);;

retourne l’entier 2.

Les tableaux sont très utilisés en pratique pour implémenter d’autres structures de données, comme par exemple les tas ou les structures Union-Find, qui seront abordées dans de prochains articles.

Exercices

Exercice de programmation : En OCaml, les listes et les tableaux sont évidemment présents, et ces deux structures sont implémentées de façon différente (contrairement à Python, par exemple) :

// La liste contenant les entiers 1, 2, et 3
let liste = [1; 2; 3];;
// Le tableau contenant les entiers 1, 2 et 3
let tableau = [|1; 2; 3|];;

(Re)programmez les primitives de ces deux structures de données : initialisation d’un objet sans données, suppression d’un élément à une position donnée (sans erreur, donc en particulier en vérifiant que l’objet contient effectivement au moins un élément !), ajout d’un élément à une position donnée, retour de la valeur ‘Vrai’ (“true” en OCaml) d’un élément dans l’objet s’il y est présent, sinon de la valeur ‘Faux’ (“false”). Ne pas utiliser les fonctions déjà présentes en OCaml…

TOUTES les fonctions que vous écrirez pour les listes auront la forme suivante :

let rec fonction argument1 argument2 ... = match argument with
| Cas 1 (when ... = ...) -> Action 1
| Cas 2 (when ... = ...) -> Action 2
| ...
| _ -> Action par défaut;;

Et chacune de ces fonctions s’appeleront vraisemblement elle-mêmes dans l’un des cas. Les cas doivent être écrits dans l’ordre croissant de priorité : si vous voulez tester le cas où la liste est vide avant le cas où elle ne l’est pas (donc elle a un élément t suivi d’une liste q éventuellement vide), le cas “[] -> Action” devra être écrit avant le cas “t::q -> Action”.

TOUTES les fonctions que vous écrirez pour les tableaux auront la forme suivante :

let fonction argument1 argument2 ... =
	let len = longueur_tableau tableau in
	...
	let nouveau_tableau = creer_tableau tableau.(0) ... in	
	// Indice de parcours d'un tableau
	let idx = ref 0 in
	...
	// Indice de parcours d'un autre des deux tableaux
	let i = ref 0 in
	while (!i < ...) do
		...
		i := !i + 1;
	done;
	nouveau_tableau;;

Important : l’indexation des listes comme des tableaux commence à 0 en OCaml ! Autrement dit, un tableau t de longueur 3 (avec 3 éléments) sera composé des éléments t.(0), t.(1) et t.(2). Appeler l’élément t.(3) retournera une erreur ! Pour renvoyer une erreur, utilisez le mot-clé “failwith” suivi d’une chaîne de caractères (une phrase entre guillemets).

Vous avez le droit d’appeler les fonctions suivantes pour les listes (elles ne seront pas expliquées ici) :

// Retourne le premier élément de la liste (la tête)
let tete liste = match liste with
| [] -> failwith "La liste fournie en argument est vide !"
| t::q -> t;;
// Retourne la liste privée de son premier élément (la queue)
let queue liste = match liste with
| [] -> failwith "La liste fournie en argument est vide !"
| t::q -> q;;

Par exemple :

tete [1;2;3];;

retourne l’entier 1.

tete [];;

retourne “Exception: Failure “La liste fournie en argument est vide !”.”.

queue [1;2;3];;

retourne la liste [2;3].

queue [];;

retourne “Exception: Failure “La liste fournie en argument est vide !”.”.

Vous avez le droit d’appeler les fonctions suivantes pour les tableaux (elles ne seront pas expliquées ici) :

// Calcule le nombre d'éléments dans le tableau
let longueur_tableau tableau = 
	let len = ref 0 in
	try (while (true) do let _ = tableau.(!len) in len := !len + 1; done; 1) with
		| _ -> !len;;
// Crée un tableau initialisé de longueur n
// initialisé avec la valeur en argument
let creer_tableau n valeur = Array.make valeur n;;

Quand utiliser une liste ? Quand utiliser un tableau ?

• Exemple 1 Voir l’article sur les graphes pour les définitions. Un noeud est dit accessible depuis un noeud $n$ si et seulement s’il existe une suite d’arêtes ayant un noeud en commun deux à deux qui relie ce noeud à $n$. Par exemple, dans l’exemple ci-dessous :

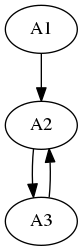
A3 et A2 sont accessibles depuis A1, mais seulement A2 est accessible depuis A3. Dans le graphe de l’exemple du dessus, tous les noeuds sont accessibles depuis n’importe quel sommet.

Etant donné un graphe, par exemple sous forme d’une matrice d’adjacence, et l’un de ses noeuds nommé $n$, on souhaite obtenir tous les noeuds accessibles depuis $n$. Pour cela, on va effectuer un parcours du graphe, c’est-à-dire que l’on va suivre toutes les arêtes accessibles depuis le noeud $n$, et stocker tous les noeuds rencontrés jusqu’à ce que l’on les ait tous vus. Par exemple, dans le graphe ci-dessus, si on part de A1, on va d’abord emprunter l’arc A1 vers A2, et stocker A2, puis l’arc A2 vers A3 (ou l’arc A2 vers A2, indifféremment) et on stocke A3 (on ne restocke pas A2, puisqu’on l’aura déjà vu, puis on empruntera l’arc A2 vers A3). A ce moment-là, on arrête le parcours, car on aura vu tous les noeuds.

Quelle serait la meilleure structure (entre le tableau et la liste) pour stocker les noeuds vus lors d’un tel parcours ? Justifier.

• Exemple 2 Vous cherchez un certain type d’objet dans un magasin très, très grand. La personne en charge du magasin vous fournit un fichier contenant l’inventaire de tous les types d’objets disponibles pour vous faciliter la tâche, ordonné par identifiant entier croissant (par exemple, il peut commencer par 1 : les abats-jours, 2 : les armoires, 5 : les tables). Comme le magasin est très grand, l’inventaire est très long et il y a un très grand nombre de types d’objets disponibles (et tous les identifiants ne sont pas peut-être tous présents, comme dans l’exemple précédent où il manque des objets de type 3 et 4). Une première méthode serait de parcourir une à une toutes les lignes de l’inventaire jusqu’à trouver la ligne associée au type d’objet que vous cherchez. Ce serait extrêmement pénible, car long. Une méthode potentiellement plus rapide, et qui utilise le fait que la liste soit ordonnée est la recherche par dichotomie. A chaque étape de l’algorithme, on divise par deux l’espace de recherche (c’est-à-dire le nombre de lignes restant à vérifier) de la façon suivante : considérant l’inventaire réduit à un certain nombre de lignes $m$, on lit la ligne numéro $\frac{m}{2}$ (ou le nombre entier le plus proche), et on compare l’identifiant présent à cette ligne avec l’entier que l’on recherche (par exemple, 42, l’indice pour les casseroles en cuivre) :

• Si cet identifiant est égal à 42, alors on a trouvé la bonne ligne;

• S’il est plus petit, alors on recherchera à la prochaine étape dans la moitié de l’inventaire qui contient les identifiants plus grand que l’identifiant courant (les $m/2$ lignes suivantes par exemple);

• S’il est plus grand, alors on recherchera à la prochaine étape dans la moitié de l’inventaire qui contient les identifiants plus petit que l’identifiant courant (les $m/2+1$ lignes précédentes par exemple).

Par exemple, pour l’inventaire (petit ici) suivant :

• 1 : abats-jours;

• 2 : armoires;

• 5 : tables;

• 40 : verres;

• 41 : casseroles en cuivre;

• 42 : poêles.

Comme l’inventaire est de taille 6 à la première étape, on lit la ligne numéro 3 : l’identifiant est 5 plus petit que 42. Donc on regarde les trois lignes suivantes, et on lit la ligne numéro 5 : l’identifiant est 41, plus petit que 42. On se limite à la dernière ligne, dont l’identifiant est 42.

Quelle serait la meilleure structure (entre le tableau et la liste) pour effectuer une recherche par dichotomie ? Justifier.

Modification du 20/02/2018: Correction de quelques tournures de phrase.