Note : C’est la correction des exercices de l’article “Introduction aux graphes”.

Exercices de compréhension

Exercice 1 : Dites combien vaut $\chi$(G) (le nombre chromatique de G) quand G a trois sommets 0, 1 et 2, et trois arêtes, une reliant 0 à 1, une reliant 1 à 2, et l’autre reliant 2 à 0.

Attention : on parle ici d’arêtes, donc le graphe est non orienté. On rappelle que $\chi$(G) est le nombre minimal de couleurs nécessaire pour qu’il existe une coloration c telle que (P) : si les sommets i et les sommets j sont reliés par une arête, alors ils ont des couleurs distinctes par la coloration c : c(i) différent de c(j) (en reprenant les notations de l’article précédent). On va évidemment utiliser au moins une couleur, donc $\chi$(G) est au moins supérieur à 1. D’autre part, de manière générale (pour toute valeur de n), le nombre minimal de couleurs est tout d’abord forcément inférieur au nombre de noeuds du graphe, ici 3, puisqu’une coloration donne une couleur à chaque noeud. Donc pour n’importe quel graphe à n sommets, 1 $\leq$ $\chi$(G) $\leq$ n.

Voici ci-dessous le graphe G de l’exercice :

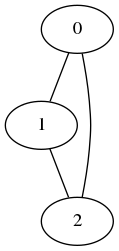
Voici un exemple de l’inégalité prouvée précédemment sur G :

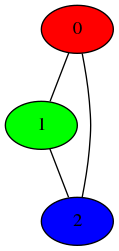
Pour montrer que $\chi$(G) = 3, il suffit donc de montrer que $\chi$(G) est supérieur à trois. Pour cela, on peut tester les cas $\chi$(G) = 1 et $\chi$(G) = 2, et montrer que de telles colorations ne respectent pas la propriété requise (P).

Pour rédiger plus proprement, on peut raisonner par la contraposée. En supposant que $\chi$(G) est strictement inférieur à 3, il existe alors deux noeuds dans G qui ont la même couleur (puisqu’il y a moins de 3 couleurs pour 3 noeuds : on appelle ce raisonnement le principe des tiroirs). Or toute paire de sommets dans G est reliée par une arête (voir le schéma précédent), donc (P) n’est pas respectée. Donc, en utilisant la contraposée, si (P) est respectée, alors $\chi$(G) est supérieur à 3. Donc $\chi$(G) = 3.

Exercice 2 : Un graphe complet à i sommets (noté $K_i$) est un graphe tel qu’il existe une arête entre chaque couple de sommets distincts du graphe (par exemple, le graphe de l’exercice précédent s’appelle $K_3$). Montrez que $\chi(K_i)$ est supérieur à i. (Indice : démonstration par l’absurde, en supposant que $\chi(K_i)$ est strictement inférieur à i)

Utilisons l’indice donné, et faisons une démonstration par l’absurde, en supposant $\chi(K_i)$ strictement inférieur à i. Alors le graphe $K_i$ est colorié avec strictement moins de i couleurs, donc il existe au moins deux noeuds distincts ayant la même couleur (voir le raisonnement effectué à l’exercice 1). Or il existe une arête entre chaque couple de sommets distincts, donc la coloration ne respecte pas (P). Donc $\chi(K_i)$ est supérieur à i.

En utilisant le raisonnement décrit à l’exercice précédent et le fait que $K_i$ a i sommets, on montre que $\chi$($K_i$)est inférieur à i, donc $\chi$($K_i$) = i.

Exercice 3 : Un cycle à i sommets $C_i$ est un graphe tel que, si les sommets sont numérotés 0, 1, 2, 3, …, i-1, ses arcs sont (0, 1), (1, 2), (2, 3), …, (i-2, i-1), (i-1, 0). Montrez que si i est supérieur à 2, alors soit $\chi(C_i)$ = 2 si i est pair, soit $\chi(C_i)$ = 3 si i est impair. (Indice : commencer par montrer qu’une couleur ne suffit pas et que si i est impair alors deux couleurs ne suffisent pas; puis donner une coloration qui vérifie (P) avec deux couleurs si i est pair, avec trois couleurs si i est impair).

Remarquons tout d’abord que $\chi$($C_i$) est supérieur à 1 (voir le raisonnement utilisé dans l’exercice 1). De plus, comme i est supérieur à 2, alors il y a au moins deux sommets dans ce graphe, et aucun des sommets du graphe n’est isolé (chacun est relié à un autre sommet par une arête/arc) d’après la définition du graphe. Donc, si on n’utilise qu’une seule couleur, alors en considérant les deux sommets 0 et 1 de la même couleur reliés par l’arc (0, 1), la propriété (P) n’est pas respectée.

Si i est impair, comme précédemment il faut que 0 et 1 aient deux couleurs différentes, mettons rouge et bleu respectivement. Essayons de colorier $C_i$ avec deux couleurs en respectant (P) : 2 va être rouge car 1 est bleu et (1,2) est un arc; 3 va être bleu car 2 est rouge et (2,3) est un arc; par un raisonnement par récurrence on obtient que i-1 doit être rouge (car i-1 est pair). Mais 0 est rouge et (0,i-1) est un arc : la seule coloration qui aurait pu vérifier (P) ne vérifie pas (P). $\chi$($C_i$) est donc supérieur ou égal à 3.

Si i est pair, colorions les noeuds de numéro pair en rouge, et les noeuds de numéro impair en bleu. Les arcs (0, 1), (1, 2), (2, 3), …, (i-2, i-1), (i-1, 0) relient toujours un noeud de numéro pair et un noeud de numéro impair, donc un noeud rouge et un noeud bleu, donc (P) est vérifiée. Ainsi $\chi$($C_i$) = 2.

Si i est impair, colorions i-1 en jaune, les autres sommets pairs en rouge, et les sommets impairs en bleu. (0,1),(1, 2), (2, 3), …, (i-3, i-2) relient toujours un noeud de numéro pair différent de i-1 et un noeud de numéro impair, donc un noeud rouge et un noeud bleu, (i-2,i-1) relie un noeud bleu et un noeud jaune et (i-1,0) relie un noeud jaune et un noeud rouge, donc (P) est vérifiée. Ainsi $\chi$($C_i$) = 3.

Exercices avancés

Exercice de programmation : Ecrire (dans le langage de votre choix) un algorithme de coloration de graphe naïf qui permet de colorier l’instance présentée précédemment dans l’article. Vérifiez qu’il renvoie bien m=2 pour l’instance présentée dans l’article. Montrer manuellement que pour le graphe G avec les noeuds $a$, $b$, $c$, $d$, $e$, et $f$ (donnés dans cet ordre), et les arêtes $(a, e)$, $(a, f)$, $(b, d)$, $(b, f)$, $(c, d)$ et $(c, e)$, l’algorithme retourne $m=2$ (ce qui est conforme à une coloration minimale faite manuellement), mais que si les noeuds sont fournis dans l’ordre $a$, $d$, $b$, $e$, $c$ et $f$, l’algorithme retourne m=3 (ce qui montre que cet algorithme n’est pas correct !).

La correction est donnée dans le langage Python, choisi pour sa lisibilité (voir ici pour la documentation et un didacticiel en français pour Python). On rappelle brièvement la méthode suivie dans l’article associé : étant donné un graphe G=(S, A) (représentés respectivement en Python par une liste d’entiers, et par une liste de couples d’entiers), on énumère les possibles nombres chromatiques en partant de 0, jusqu’à trouver une coloration qui respecte la propriété (P) sur l’ensemble du graphe. L’algorithme retourne le nombre chromatique m correspondant. Le plus dur est d’implémenter la procédure de coloration du graphe. En pratique, au lieu de fixer d’abord $m$ et d’essayer de colorier le graphe, on va plutôt partir d’un noeud que l’on va colorier par exemple en bleu (couleur 1); on coloriera ses voisins en jaune (couleur 2). On va alors répéter ce processus, quitte à utiliser d’autres couleurs lorsque au moins l’un des voisins du noeud que l’on considère est colorié en bleu, jaune, ou toute autre couleur déjà utilisée. La coloration sera résumée dans un tableau de longueur égale au nombre de noeuds dans le graphe, et où sera écrit dans chaque case associée à un noeud le numéro correspondant à la couleur de ce noeud. On garde en mémoire le nombre de couleurs utilisé $m$.

def trouver_coloration_naif(S,A):
	## Si le graphe est vide ##
	if (len(S)==0):
		return(0)
	## Initialisation du     ##
	## tableau de couleurs   ##
	## de taille |noeuds|    ##
	col=[None]*len(S)
	## Comme le graphe n'est ##
	## pas vide, il y a au   ##
	## moins une couleur     ##
	m = 1
	## Si le graphe ne       ##
	## contient qu'un seul   ##
	## sommet ou ne possède  ##
	## aucune arête (on dit  ##
	## que les sommets de ce ##
	## graphe sont isolés    ##
	if (len(A)==0):
		return(m)
	i = 0
	## Tant que tous les     ##
	## noeuds ne sont pas    ##
	## coloriés              ##
	while (any([v==None for v in col]) and i < len(S)):
		## Les voisins du noeud d'indice i sont les noeuds qui ##
		## partagent une arête/arc avec ce noeud              ##
		## On récupère ici tous les sommets entrants ayant    ##
		## une arête/arc en commun avec le sommet S[i]        ##
		voisins = [S.index(x[1]) for x in filter(lambda x : x[0]==S[i], A)]
		## On récupère ici tous les sommets sortants ayant    ##
		## une arête/arc en commun avec le sommet S[i]        ##
		voisins += [S.index(x[0]) for x in filter(lambda x : x[1]==S[i], A)]
		M = 1
		## On trie les couleurs des voisins par ordre         ##
		## croissant pour valider la boucle suivante :        ##
		colVoisins = sorted([col[v] for v in voisins])
		## Sinon, on peut imaginer le cas où on ne voit que   ##
		## des voisins coloriés avec la couleur 2 (pour M=1)  ##
		## puis un voisin colorié avec la couleur 3 (M=2)     ##
		## donc la coloration ne respecte pas la propriété (P)##
		## pour les voisins précédents                        ##
		## Tant qu'il existe un noeud voisin de S[i] colorié  ##
		## avec la couleur M, tester la couleur M+1           ##
		while (any([c==M for c in colVoisins])):
			M += 1
		## Si toutes les couleurs existantes ont déjà été     ##
		## utilisées pour au moins un noeud voisin de S[i]    ##
		## alors on crée une nouvelle couleur                 ##
		if (M == m+1):
			m += 1
		## On choisit finalement la couleur du noeud S[i]     ##
		col[i] = M
		i += 1
	return(m)

Pour tester l’instance du problème de l’article précédent :

## Initialiser les noeuds ##
S=["Mathématiques", "Français", "Histoire", "SVT", "Physique"]
## Initialiser les arêtes ##
A=[["Mathématiques", "Français"], ["Histoire", "SVT"], ["SVT", "Physique"]]
## Lancer l'algorithme    ##
print(trouver_coloration_naif(S, A))

L’algorithme retourne bien m=2 sur cette instance. Si on choisit de retourner aussi le tableau col, on a un exemple de coloration minimale (i.e. une coloration qui respecte la propriété (P) avec un nombre minimal de couleurs) pour le graphe en entrée. Cette coloration n’est pas forcément unique !

Pour tester le contre-exemple donné :

## Ordre donnant m = 2 ##
S=["a", "b", "c", "d", "e", "f"]
A=[["a", "e"], ["a", "f"], ["b", "d"], ["b", "f"], ["c", "d"], ["c", "e"]]
print(trouver_coloration_naif(S, A))

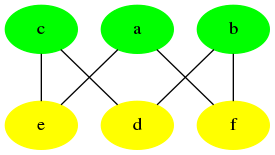
## Ordre donnant m = 3 ##
S=["a", "d", "b", "e", "c", "f"]
print(trouver_coloration_naif(S, A))

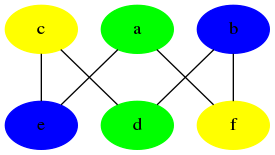
De manière générale, le graphe de noeuds (1, 2, 3, …, $n$) pour un entier $n$ pair strictement supérieur à 2, et d’arêtes (1, $\frac{n}{2}+2$), …, (1, $n$), (2, $\frac{n}{2}+1$), (2, $\frac{n}{2}+3$), …, ($\frac{n}{2}$, $\frac{n}{2}+1$), ($\frac{n}{2}$, $\frac{n}{2}+2$), …, ($\frac{n}{2}$, $n-1$) s’appelle un graphe couronne d’ordre $n$ (on met les noeuds 1 à $\frac{n}{2}$ à gauche en colonne, les noeuds $\frac{n}{2}+1$ à $n$ à droite en colonne, et pour un noeud donné à gauche, on le relie à tous les noeuds à droite sauf à celui qui lui fait face). Ce contre-exemple est attribué à D. S. Johnson, dans son article de 1974 appelé “Worst-case behavior of graph coloring algorithms” (“Comportement dans le pire des cas des algorithmes de coloration de graphe”).

Le problème de coloration de graphe est complexe; en particulier, trouver le nombre minimal de couleurs nécessaire pour colorier un graphe arbitraire est déjà compliqué ! Une méthode possible pour s’assurer de trouver une coloration de graphe qui est bien minimale, contrairement à celle que peut renvoyer l’algorithme naïf ci-dessus, est de tester pour $m$ allant de 1 à $n$ (où $n$ est le nombre de noeuds du graphe, qui est également le nombre maximal de couleurs avec lesquelles on peut colorier ce graphe !), si le graphe est coloriable avec $m$ couleurs. Par exemple, une manière simple d’implémenter ceci est de tenter de colorier le graphe avec $m$ couleurs en coloriant un premier noeud $u$, en gardant la contrainte “ne pas colorier avec la même couleur que $u$” sur les noeuds voisins directs de $u$, et de recommencer cette procédure sur les voisins de $u$, puis sur leurs propres voisins, etc. jusqu’à arriver jusqu’à un graphe correctement colorié, ou une contradiction (un noeud qui ne peut pas être colorié car toutes les contraintes sur les $m$ couleurs sont présentes). Dans ce dernier cas, on revient au dernier moment où le graphe était correctement (partiellement) colorié, et on change la couleur appliquée au noeud que l’on avait colorié à cette étape. Si au terme de toutes les étapes de “retour en arrière” possibles, on retombe quand même sur une contradiction, cela veut dire que le graphe n’est pas coloriable avec $m$ couleurs, et on passe à m+1 couleurs.

Cette étape de “retour en arrière” s’appelle “backtracking”, et sera détaillée, en même temps que l’algorithme que l’on décrit, dans un prochain article.

Une famille de graphes particulière : les graphes planaires Un graphe planaire G est tel qu’il existe une façon de le dessiner sans que les arêtes ne s’intersectent. Un graphe planaire plongé est un graphe qui est dessiné sans que les arêtes ne s’intersectent. Autrement dit, un graphe planaire peut être dessiné sous forme d’un graphe planaire plongé. Ici, lorsqu’on évoquera un graphe planaire, on pensera à sa version plongée.

Le graphe $K_4$ est-il planaire ? $K_5$ est-il planaire ? (Indice : il y a un oui et un non. Pour prouver le oui, dessinez une version planaire du graphe. La justification du non nécessite le théorème de Kuratowski-Wagner, qui sera présenté plus tard)

$K_4$ est planaire, voir le dessin ci-dessous :

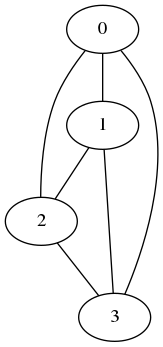
Une autre famille de graphes particulière : les graphes connexes Un graphe connexe est un graphe tel que, pour tous sommets i et j distincts, il existe un chemin, c’est-à-dire une suite d’arêtes/arcs, dans le graphe de i vers j (et de j vers i, si le graphe est non orienté). Par exemple, $K_3$ est connexe. Donnez un exemple de graphe non connexe, et justifiez sa non-connexité (On exhibera donc un couple de sommets qui ne respecte pas la condition ci-dessus).

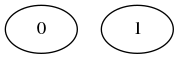
0 et 1 ne respectent pas la condition de connexité, puisque ce graphe ne possède pas d’arête.

Une autre famille de graphes particulière : les graphes bipartis Le graphe $G_{i,j}$ est le graphe constitué de deux ensembles de sommets distincts $G_i$ (contenant i sommets) et $G_j$ (contenant j sommets), tels que toute arête/arc soit une interaction de la forme (a, b) où soit a appartient à $G_i$ et b appartient à $G_j$, soit a appartient à $G_j$ et b appartient à $G_i$. Vérifiez que le graphe présentant l’instance du problème de l’article est un graphe biparti, et exhibez les parties de l’ensemble de sommets correspondantes. Il existe un théorème qui montre qu’un graphe a un nombre chromatique inférieur à 2 si et seulement s’il est biparti. Prouvez ce théorème.

Le graphe est bien biparti : on colore les noeuds du premier ensemble de sommets en rouge, ceux du deuxième ensemble en vert.

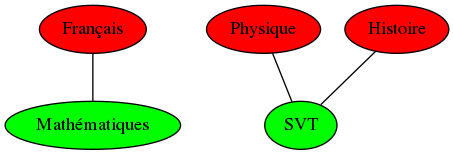
L’énoncé du théorème utilise un “si et seulement si” : il s’agit alors de prouver les deux sens de l’équivalence.

Supposons que le graphe est biparti. Alors colorions en rouge les noeuds issus du premier ensemble de sommets, et en vert les noeuds appartenant au deuxième ensemble (comme dans la figure ci-dessus). Alors la coloration obtenue respecte bien la propriété (P) de l’article d’introduction aux graphes (car les deux ensembles de sommets sont distincts et que les arêtes/arcs ne sont partagés que par des noeuds appartenant à des ensembles de sommets différents, par définition).

Supposons que le graphe a un nombre chromatique inférieur à 2, donc égal à 1 ou à 2 si le graphe possède au moins un sommet. S’il est égal à 1, alors cela signifie que les noeuds du graphe ne sont pas reliés entre eux, car s’il existait une arête/arc, alors la propriété (P) ne serait pas maintenue pour le couple de noeuds reliés par cette arête/arc. On peut alors choisir arbitrairement deux ensembles de sommets distincts (avec éventuellement l’un des deux vide) dont l’union est égale à l’ensemble total de sommets, donc le graphe est biparti. Si le nombre chromatique est égal à 2, alors il existe une coloration à deux couleurs du graphe qui respecte la propriété (P). Les deux ensembles de noeuds distincts sont alors les deux ensembles de noeuds de couleur différente. Par définition de la coloration, les arêtes/arcs ne relient que des noeuds de couleur différente, donc appartenant à des ensembles différents. Donc le graphe est biparti.

Bonus : Pour dessiner les graphes, on peut utiliser GraphViz (ce qui a été utilisé pour cet article). Voir cette référence pour une première approche.

Modifications du 30/12/2017 : Correction de quelques tournures de phrases; commentaire de l’algorithme en Python. Modification de la démonstration de l’exercice 3 (merci à Clémentine Lemarié-Rieusset).

Modifications du 22/01/2018 : Correction du commentaire de l’algorithme (le cas “len(A) == 0” s’applique aussi à un ensemble de sommets isolés de taille arbitraire). Correction d’une tournure de phrase. Ajout du résultat d’existence d’une coloration minimale retournée par l’algorithme.

Modifications du 15/09/2018 : Ajout du contre-exemple de Johnson dans l’exercice de programmation.