Note : Les quatre premiers articles de mathématiques peuvent être utiles pour faire les exercices de cet article (ne vous inquiétez pas, ils sont très courts !).

Un graphe est un objet mathématique qui permet, notamment, de représenter une communauté et ses interactions : par exemple, un groupe de profils Facebook avec les ajouts en ami, un ensemble de villes et les routes qui les relient entre elles, un ensemble de gènes et leurs liens de régulation, … Il s’agit dans cet article d’introduire les définitions basiques portant sur les graphes pour résoudre un problème simple : étant donné des emplois du temps scolaires dans une école, compter le nombre de salles nécessaires à réserver pour que tous les cours soient mis en place. Le problème majeur est que plusieurs cours peuvent avoir lieu simultanément, et réserver une salle est suffisamment pénible pour souhaiter n’avoir à le faire qu’un nombre minimal de fois (sinon attribuer autant de salles qu’il y a de cours aurait été une solution acceptable).

Il y a une distinction importante à faire entre un problème et une instance de ce problème. Une instance de ce problème est un exemple concret d’un problème : par exemple, la description abstraite ci-dessus est un problème. Une instance de ce problème serait de se donner un véritable emploi du temps (avec heures et intitulés des cours), et trouver la solution pour cette instance particulière d’emploi du temps. Dire que “entiers” est un ensemble de nombres avec des propriétés particulières, et que 1, 2, 3, … sont des instances de nombres entiers est analogue.

Définitions

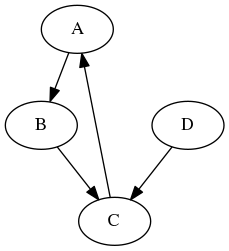
Commençons par définir ce qu’est exactement un graphe (voir un exemple simple de graphe ci-dessus). Comme écrit précédemment, un graphe représente un ensemble d’objets et les interactions entre ces objets : on appelle les objets des sommets (ou noeuds). Une interaction est symétrique si, quand l’objet A interagit avec B, nécessairement B interagit également avec A; sinon cette interaction est dite asymétrique. Par exemple, pour les amis sur Facebook, si Alice est amie avec Bob, alors Bob est aussi ami avec Alice. Au contraire, dans le cas d’un arbre généalogique, si Charlotte est la mère de Daniel, en revanche Daniel n’est pas la mère de Charlotte. Si vous êtes familiers avec les relations en mathématiques (par exemple, l’égalité, les ordres, …), les graphes peuvent être la représentation d’un relation d’ordre sur des éléments d’un ensemble.

Dans un graphe, on appelle les interactions symétriques (ou non orientées) arêtes, et les interactions asymétriques (ou orientées) arcs.

Un graphe est caractérisé par les ensembles de ses sommets (à renommage près) et de ses interactions : c’est-à-dire que si on possède ces deux informations, alors on peut reconstruire le graphe de façon non ambiguë, quitte à changer le nom des sommets si nécessaire. On écrit souvent, comme définition d’un graphe G : G = (S, A) où S est l’ensemble des sommets, et A l’ensemble des arêtes/arcs.

Par exemple, pour le graphe ci-dessus, l’ensemble des sommets est { A, B, C, D } et les arcs sont (A, B), (B, C), (C, A) et (D, C). Le premier sommet écrit pour un arc donné est le sommet sortant, et le deuxième le sommet entrant : par exemple, A est le sommet sortant de (A,B), et B en est le sommet entrant.

Le degré d’un noeud/sommet du graphe est le nombre d’interactions qui impliquent ce noeud. Si les interactions ne sont pas symétriques, on définit séparément le degré entrant, donc le nombre d’interactions qui ont ce noeud pour sommet entrant, et le degré sortant, le nombre d’interactions qui ont ce noeud pour sommet sortant. Par exemple, ici A a un degré entrant égal à 1. Son degré sortant est également égal à 1.

La notion de coloration

Maintenant on va utiliser les graphes définis précédemment dans notre problème d’attribution de salles. Etant donné notre emploi du temps d’un jour donné, on va se saisir de notre boîte à crayons, et colorier chaque cours avec une couleur différente si une nouvelle salle a besoin d’être attribuée. Décrivons une instance de ce problème à l’aide d’un graphe.

Voici notre emploi du temps, où les cours sont présentés par ordre chronologique :

Cours	Horaires
Français	8H30 - 11H00
Mathématiques	9H30 - 12H00
Physique	13H00 - 14H30
Sciences de la Vie et de la Terre	14H00 - 18H00
Histoire	14H40 - 16H00

Chaque sommet sera un cours de l’emploi du temps. Chaque arête entre deux sommets sera présente ssi (si et seulement si) les cours associés à ces sommets se déroulent en même temps/se superposent dans le temps. C’est bien une interaction symétrique.

Voici le graphe correspondant :

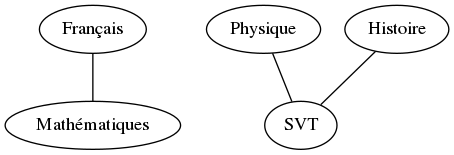
Maintenant définissons une coloration d’un graphe :

Une coloration d’un graphe est une fonction notée c qui à un sommet associe sa couleur : par exemple, si on a colorié le sommet “Français” du graphe en bleu, c(“Français”) = “bleu”. On utilisera par la suite pour plus de confort des entiers pour désigner les couleurs : par exemple, le rouge est associé à 0, le bleu à 1, etc. Il est évidemment préférable d’associer deux entiers différents à deux couleurs différentes ! En définitive, c sera une fonction d’un intervalle {1, 2, …, n} dans un intervalle {1, 2, …, m}, où n sera le nombre de sommets, qui sont nommés 0, 1, 2, … jusqu’à n, et m le nombre de couleurs, et c(i) sera donc la couleur du sommet numéroté i, où i est un entier.

Définissons la propriété de non-superposition des couleurs :

Propriété (P) : Si les sommets i et les sommets j sont reliés par une arête alors ils ont des couleurs distinctes par la coloration c : c(i) est différent de c(j).

Enfin, définissons une coloration minimale d’un graphe.

Une coloration minimale d’un graphe est une coloration qui utilise le moins de couleurs possible tout en respectant la propriété (P) : autrement, où m est le plus petit possible. On notera $\chi$(G) cette valeur minimale de m, que l’on appelle nombre chromatique (du grec khrôma $\chi\rho\omega\mu\alpha$, qui signifie “peau”, et par extension “couleur de peau”, “couleur”).

Résolution

Essayons de trouver une solution naïve à l’instance du problème décrite ci-dessus. En particulier, on recherche une solution algorithmique, c’est-à-dire une suite d’instructions “simples”, avec éventuellement des répétitions, que l’on pourra fournir à un ordinateur.

Puisque cette instance est de petite taille, on peut énumérer les nombres de couleurs en partant de 1, et incrémenter (i.e. augmenter d’une unité à chaque étape) ce nombre jusqu’à trouver un nombre de couleurs qui respecte la propriété (P). Comme on aura énuméré les nombres de couleurs dans l’ordre croissant, nous serons certains que ce nombre trouvé sera minimal.

Une chose à vérifier est s’il existe une coloration minimale de ce graphe (parce que sinon nous énumérerons sans fin tous les entiers…). Dans ce cas-ci, c’est assez évident puisque, comme dit précédemment, une solution non minimale mais acceptable au problème est de réserver autant de salles qu’il y a de cours. Autrement dit, choisir autant de crayons de couleur qu’il y a de cours. Donc, au maximum, nous énumérerons 1, 2, 3, 4, 5 (car 5 est le nombre total de cours). Il est à noter que dans d’autres situations, savoir que notre procédure a une fin n’est pas aussi évident, mais que cela reste tout aussi crucial à savoir. La propriété qu’une procédure (en fait, un algorithme) termine, c’est-à-dire, qui a une fin, est la terminaison d’un algorithme.

Montrons que pour notre exemple, le nombre de couleurs minimal à utiliser est 2. On va énumérer le nombre de couleurs dans l’ordre croissant jusqu’à trouver un nombre de couleurs qui permette de colorier le graphe en respectant la propriété (P). Par définition, il sera le nombre minimal qui permette de colorier le graphe.

Cas m=1 (où on n’utilise qu’une couleur) : Si on ne choisit qu’une seule couleur, alors on voit que la propriété (P) ne sera pas respectée par exemple pour le couple de sommets Français et Mathématiques : voir l’arête (Français, Mathématiques).

Cas m=2 (où on n’utilise que deux couleurs) : La propriété (P) est vérifiée !

Un exemple de coloration (pas forcément unique !) pour m=2 est présenté ci-dessous :

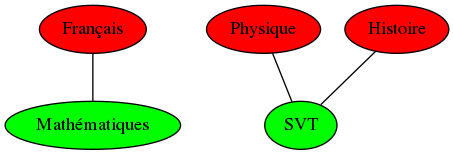
Attention : La méthode naïve proposée au-dessus n’est pas correcte ! La correction d’un algorithme est la propriété qu’il retourne le bon résultat pour toute entrée, et c’est la deuxième propriété importante à démontrer dans un algorithme avec la terminaison. En l’occurrence, pour voir un contre-exemple à la solution que l’on a proposé, voir l’exercice de programmation dans la catégorie “Exercices avancés”.

Exercices de compréhension

Quelques exercices pour vérifier votre compréhension de l’article. La correction de tous les exercices sera donnée dans le prochain article :

Exercice 1 : Dites combien vaut $\chi$(G) quand G a trois sommets 0, 1 et 2, et trois arêtes, une reliant 0 à 1, une reliant 1 à 2, et l’autre reliant 2 à 0.

Exercice 2 : Un graphe complet à i sommets (noté $K_{i}$) est un graphe tel qu’il existe une arête entre chaque couple de sommets distincts du graphe (par exemple, le graphe de l’exercice précédent s’appelle $K_3$). Montrez que $\chi(K_{i})$ est supérieur à i. (Indice : démonstration par l’absurde, en supposant que $\chi(K_{i})$ est strictement inférieur à i)

Exercice 3 : Un cycle à i sommets $C_i$ est un graphe tel que, si les sommets sont numérotés 0, 1, 2, 3, …, i-1, ses arêtes sont (0, 1), (1, 2), (2, 3), …, (i-2, i-1), (i-1, 0). Montrez que si i est supérieur à 2, alors soit $\chi(C_i)$ = 2 si i est pair, soit $\chi(C_i)$ = 3 si i est impair. (Indice : raisonnement par récurrence sur i puis, à l’intérieur de la récurrence, un raisonnement par disjonction de cas, dans les deux cas où i est pair/impair)

Exercices avancés

Exercice de programmation : Ecrire (dans le langage de votre choix) un algorithme de coloration de graphe naïf qui permet de colorier l’instance présentée précédemment dans l’article. Vérifiez qu’il renvoie bien m=2 pour l’instance présentée dans l’article. Montrer manuellement que pour le graphe G avec les noeuds $a$, $b$, $c$, $d$, $e$, et $f$ (donnés dans cet ordre), et les arêtes $(a, e)$, $(a, f)$, $(b, d)$, $(b, f)$, $(c, d)$ et $(c, e)$, l’algorithme retourne $m=2$ (ce qui est conforme à une coloration minimale faite manuellement), mais que si les noeuds sont fournis dans l’ordre $a$, $d$, $b$, $e$, $c$ et $f$, l’algorithme retourne m=3 (ce qui montre que cet algorithme n’est pas correct !).

Une famille de graphes particulière : les graphes planaires Un graphe planaire G est tel qu’il existe une façon de le dessiner sans que les arêtes ne s’intersectent. Un graphe planaire plongé est un graphe qui est dessiné sans que les arêtes ne s’intersectent. Autrement dit, un graphe planaire peut être dessiné sous forme d’un graphe planaire plongé. Ici, lorsqu’on évoquera un graphe planaire, on pensera à sa version plongée.

Le graphe $K_4$ est-il planaire ? $K_5$ est-il planaire ? (Indice : il y a un oui et un non. Pour prouver le oui, dessinez une version planaire du graphe. La justification du non nécessite le théorème de Kuratowski-Wagner, qui sera présenté plus tard)

Une autre famille de graphes particulière : les graphes connexes Un graphe connexe est un graphe tel que, pour tous sommets i et j distincts, il existe un chemin, c’est-à-dire une suite d’arêtes, dans le graphe de i vers j (et de j vers i, si le graphe est non orienté). Par exemple, $K_3$ est connexe. Donnez un exemple de graphe non connexe, et justifiez sa non-connexité (On exhibera donc un couple de sommets qui ne respecte pas la condition ci-dessus).

Une autre famille de graphes particulière : les graphes bipartis Le graphe $G_{i,j}$ est le graphe constitué de deux ensembles de sommets distincts $G_i$ (contenant i sommets) et $G_j$ (contenant j sommets), tels que toute arête/arc soit une interaction de la forme (a, b) où soit a appartient à $G_i$ et b appartient à $G_j$, soit a appartient à $G_j$ et b appartient à $G_i$. Vérifiez que le graphe présentant l’instance du problème de l’article est un graphe biparti, et exhibez les parties de l’ensemble de sommets correspondantes. Il existe un théorème qui montre qu’un graphe a un nombre chromatique inférieur à 2 si et seulement s’il est biparti. Prouvez ce théorème.

Modifications du 18/12/2017 : Changements mineurs dans les notations.

Modifications du 21/12/2017 : Ajout de détails pour expliquer pourquoi une couleur peut être représentée par un entier.

Modifications du 30/12/2017 : Correction de quelques tournures de phrases; ajout d’un exemple pour les sommets sortants/entrants.

Modifications du 14/09/2018 : Ajout de la propriété de correction d’un algorithme. Entête avant la démonstration m=2 pour l’instance de graphe présentée dans l’article. Ajout du contre-exemple de Johnson dans l’exercice de programmation.